티스토리 뷰
[논문 리뷰] AdaViT: Adaptive Vision Transformers for Efficient Image Recognition
최멋 2022. 8. 30. 20:13Abstract & Introduction
Vision transformer(ViT)는 현재 다양한 computer vision 분야에서 적극적으로 사용되고 훌륭한 성능을 보이고 있습니다.
그러나 ViT는 self attention mechanism의 특성상 input image 크기 (patch의 개수)에 quadratic한 계산 복잡도를 가집니다.
이 논문은 이것을 완화하기 위해 ViT의 구성 요소인 patch / head / block을 선택적으로 사용할 수 있는 방법을 제시합니다.

그림 1은 'White Stork' 이미지의 분류를 위해 AdaViT가 주로 참조한 patch를 시각화한 것입니다. 대부분이 배경인 탓에 실제로 중요한 patch는 매우 일부에 불과합니다. 따라서 이런 쓸모없는 patch, 나아가서 head 혹은 일부 transformer layer 자체를 생략 혹은 삭제할 수 있다면 큰 연산 이득이 있겠죠.
Approach

그림 2는 AdaViT의 전체 구조도입니다. ViT의 모든 Patch / Head / Block 중 중요한 부분만을 선택하여 사용하며 Decision network를 통해 중요도를 파악합니다.
Decision network의 입력은 논문에서는 이전 transformer layer의 출력을 의미하는 $Z_l$로 표현하는데요. 그렇게 되면 뭔가 이상합니다. $Z_l$의 size는 $(Batch\, size, number\, of\, tokens, dimension)$이 될텐데 여기서 single layer perceptron인 $m^p$, $m^h$, $m^b$를 통과한 결과가 그림과 같은 1d vector가 나올 수가 없겠죠.
그래서 official code를 살펴보니...
사실은 $Z_l$이 아니라 policy token이라는 변수명으로 $Z_l$의 첫 번째 토큰인 class token을 decision network의 입력으로 쓰고 있음을 확인했습니다. 이 부분은 논문에서 좀 더 정확하게 밝혀줬어야 혼동이 없었을것 같네요. 어쨌든 이전 layer의 class token을 이용해 판단한다는 점을 염두에 두고 이후에 설명할 각 module의 내용을 이해하시면 되겠습니다.
-Patch selection module
Patch selection을 진행하기 위해서 각 레이어마다 $W^p$라는 single linear layer를 둡니다. 이 layer에 이전 layer에서 가져온 policy token(class token)을 통과시켜 $(1,N)$ ($N:patch$개수) 크기의 vector를 얻습니다. 이 vector의 k번째 자리는 이번 transformer layer에서 k번째 token의 유지 확률을 뜻합니다.
이렇게 keeping probability vector $m^p$를 얻고 나면, 이 확률로 on/off를 결정하는 binary vector인 $M^p$를 sampling합니다. 예를 들어서 $m^p$의 첫 번째 성분이 0.3이라면, $M^p$의 첫 번째 성분은 0.3의 확률로 1로 sampling, 0.7의 확률로 0으로 sampling되는거죠. ($m^p$는 sigmoid를 거치기 때문에 항상 0~1의 확률값을 가집니다.)
이 discrete sampling에 대해서는 backpropagation이 불가한데요. 이것을 해결하기 위한 trick은 각 module을 설명한 후에 따로 설명드리도록 하겠습니다.
어쨌든 이런 방식으로 $M^p$를 모두 sampling하고 나면 Patch를 선택할 수 있습니다. $M^p$의 각 성분이 binary이기 때문에 간단하게 $Z_l$과의 elementwise 곱셈을 통해 on/off를 반영할 수 있겠죠. 이는 다음과 같은 식으로 표현할 수 있습니다.

이런 식으로 미리 다음 layer에서 사용할 patch를 골라서 사용할 수 있는거죠.
-Head selection module
Head selection module에서도 patch selection module과 유사하게 $W^h$라는 single linear layer를 사용합니다. 이 layer에 이전 layer의 class token을 통과시켜 $(1,H)$ 크기($H$:Head 개수)의 1d probability vector를 얻습니다. 이 vector는 각 head의 keeping probability를 의미하겠죠.
이 논문에서는 head의 on/off 방법으로 두가지 method를 제안합니다.
1. Partial deactivation
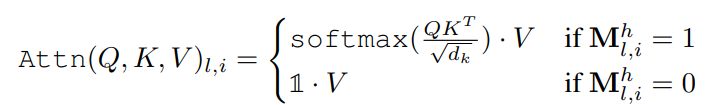
그림 3의 수식처럼 sampling된 확률이 1인 head에 대해서는 self attetnion mechanism을 적용하고, 그렇지 않은 head에 대해서는 Value transform된 값을 그대로 사용하는 것을 partial deactivation이라고 명명했습니다. 이 경우 off된 head에서는 attetnion mechanism의 동작을 억제함으로써 on/off 를 반영했는데, 개인적으로 이럴 경우 오히려 on 된 head의 값이 softmax값(0~1)이 곱해지며 다음 layer에 더 낮은 영향력을 끼치는 것이 아닌가 하는 생각이 들었습니다.
2. Full deactivation

그림 4의 수식처럼 off된 head는 모두 빼고 on된 head만을 concat하여 다음 block으로 넘겨주는 것을 full deactivation이라고 명명했습니다. 이럴 경우 기존 transformer input의 dimension이 block마다 점점 줄어 연산 이득이 계속해서 중첩되겠죠. 이에 따른 trade-off로 약간의 성능 하락은 있지만, 물리적인 dimension 크기를 줄여 큰 연산 이득을 볼 수 있습니다.
-Block selection module
Block selection의 경우도 앞선 두 module과 마찬가지로 single layer perceptron을 사용하여 probaility vector를 만듭니다. 그림 2에서 확인할 수 있듯이, 한 transformer block을 두 sublayer(MSA,FFN)으로 나누어 각각 on/off를 선택할 수 있게 합니다.
Optimization problem
앞서 말씀드린 것 처럼 discrete한 분포(binary decision)에서의 sampling은 backpropagation이 불가능합니다. 따라서 이것을 해결하기 위해 특별한 trick을 사용해야 합니다. VAE에서의 reparameterization trick을 떠올리시면 이해가 한층 수월할 것 같네요.
이 연구에서는 Gumbel softmax trick이라는 method를 사용합니다. 이를 설명하기 위해 선행 연구인 Gumbel max trick부터 설명하도록 하겠습니다.
-Gumbel Max trick
먼저 Gumbel max trick을 사용하는 이유는 discrete한 함수의 sampling을 backpropagation하기 위해서입니다. 앞서 말씀드린 이 연구에서의 sampling 방법을 생각해보면, part 각각에서 0,1이라는 값을 특정 확률로 sampling하게 됩니다. 이를 그래프로 그려보면 계단 모형의 그래프가 되어 미분이 불가하겠죠. 이를 Gumbel max trick으로 해결합니다.
어떤 categorical distribution $z$가 $zCategorical(x_1 ,...,x_k )$로 분포되어있다고 합시다. 이번 논문에서는 on/off를 나타내므로 0과 1이 될 확률, 즉 $x_1$과 $x_2$가 존재하겠죠. 이 때 Gumbel distribution의 특성을 이용해 trick을 사용합니다.
$u_k = log x_k + G_k$일 때 $P(u_k>u_j) = x_k$ , $G_k$ : Gumbel distribution
위와 같은 Gumbel distribution의 특성을 이용해 discrete한 categorical 함수를 continuous한 식으로 바꿔줄 수 있습니다. 따라서 미분이 가능해집니다!
그러나 저렇게 변환한 값들 중에서 가장 큰 값의 index만을 취하고 싶겠죠. 예를 들면 on/off 문제에서 더 확률이 높은 값을 취하는 것 처럼요. 그러기 위해서는 Gumbel max trick에서 나온 값중 argmax index $i$, 즉 가장 확률이 높게 나오는 값의 인덱스만을 취할 수 있어야하는데, 그러다보니 argmax function의 미분이 문제가 됩니다.
-Gumbel Softmax
이를 위해서 Gumbel softmax trick을 사용합니다. 이것은 기존에 존재하는 softmax temperature 개념을 Gumbel max trick과 합친 것으로 볼 수 있습니다. Temperature의 조절을 통해서 기존에 존재하는 분포를 one-hot에 가깝게 근사시키는 거죠. 정리하면, temperature의 조절은 0에 매우 근사한 temperature 설정을 통해서 가장 높은 probability를 가지는 index를 sampling할 확률을 1에 가깝게 만들어주는 역할을 합니다. 여기에 아까 전에 구해둔 Gumbel max trick을 접목함으로써 Gumbel softmax trick이 완성됩니다. 이러면 argmax function과 sampling에 대한 backpropagation이 모두 해결되겠죠?

그래서 식으로 표현하면 다음과 같이 기존 softmax에 temperature를 적용한 식 바탕으로 속에 Gumbel function이 들어가게됩니다.
수학적인 개념이라 이해하기가 쉽지 않은데..
Jang, Eric, Shixiang Gu, and Ben Poole. "Categorical reparameterization with gumbel-softmax." arXiv preprint arXiv:1611.01144 (2016).
이 논문을 바탕으로 공부하시면 도움이 되실 것 같습니다.
-Loss function
Loss function으로는 기존의 cross entropy loss에 추가하여 $L_{usage}$라는 이름의 loss를 더해 사용합니다. 이 loss의 의도는 가장 많은 patch / head / block을 생략할 수 있도록 하는 것이겠죠. 식은 다음과 같습니다.

여기서 $\gamma$는 각 patch / head / block의 통과율을 적어도 어느정도는 유지시키기 위해서 마련한 budget입니다. 아예 모든 경로를 다 block해버리면 안되니까요.
Experiment

ImageNet에 대한 실험 결과입니다. Baseline upperbound가 기존의 ViT를 의미하는데요, 0.8%의 성능 하락이 있었지만 FLOPs가 2배 이상 감소한 결과를 보입니다. Baseline Random은 말그대로 random하게 ViT의 patch / head / block을 deactivate한 상황이구요. Random+는 random하게 deactivate하며 fine-tuning을 적용했을때의 결과입니다. 아마도 이 논문에서 제시한 방법으로 deactivation을 실행했을 때 random deactivation시보다 훨씬 좋은 성능이 나오는 것을 바탕으로 타당성을 보여주는 듯 하네요.

위 그림에서 볼 수 있듯이 transformer layer가 진행됨에 따라서 점점 중요한 patch들만 activate됨을 확인할 수 있습니다. Transformer 자체가 input dependent한 model이고, 이 방법 자체도 input adaptive하게 설계한 method이기 때문에 입력마다 각 patch가 on/off되는 양상은 차이가 있음을 확인할 수 있습니다.
이외에도 다양한 실험 결과가 존재하고, 특히 visualization을 포함한 분석이 많이 있는 논문이기 때문에 결과에 대해서는 논문을 직접 보시면서 확인하시면 더 이해가 빠르실 듯 합니다.
이상
Meng, Lingchen, et al. "AdaViT: Adaptive Vision Transformers for Efficient Image Recognition." Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2022.
논문 리뷰였습니다.
읽어주셔서 감사합니다:)
'Vision Transformer > 기타' 카테고리의 다른 글
- Total
- Today
- Yesterday
- AdaViT
- ReID #ViT #Transformer #Person re-identification #Human parsing #SSl #Self supervised learning
- Uniformer #ViT #Vision transformer #비전트랜스포머 #컴퓨터비전 #딥러닝 #transformer #논문리뷰
- Vision transformer #컴퓨터비전 #딥러닝 #ViT #transformer #T2T #tokens to token ViT #논문리뷰
- Vision transformer #ViT #transformer #computer vision #deep learning #컴퓨터비전 #딥러닝 #트랜스포머 #비전트랜스포머
- ReID #컴퓨터비전 #딥러닝 #머신러닝 #Person Re-identification #Re-identification
- Beyond Self-attention
- CPE #컴퓨터비전 #딥러닝 #머신러닝 #Transformer #Vision transformer #ViT #Positional encoding
- Transformer Meets Part Model #ViT #Vision transformer #컴퓨터비전 #논문 리뷰 #딥러닝
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
